Informatique – L'Œil de l'observateur

Théorie de l’information

The Information Bottleneck Method for Optimal Prediction of Multilevel Agent-based Systems

Robin Lamarche-Perrin, Sven Banisch, and Eckehard Olbrich. In Advances in Complex Systems, vol. 19, n°1 & 2, p. 1650002-1-45. World Scientific Publishing Company, Singapore, 2016.

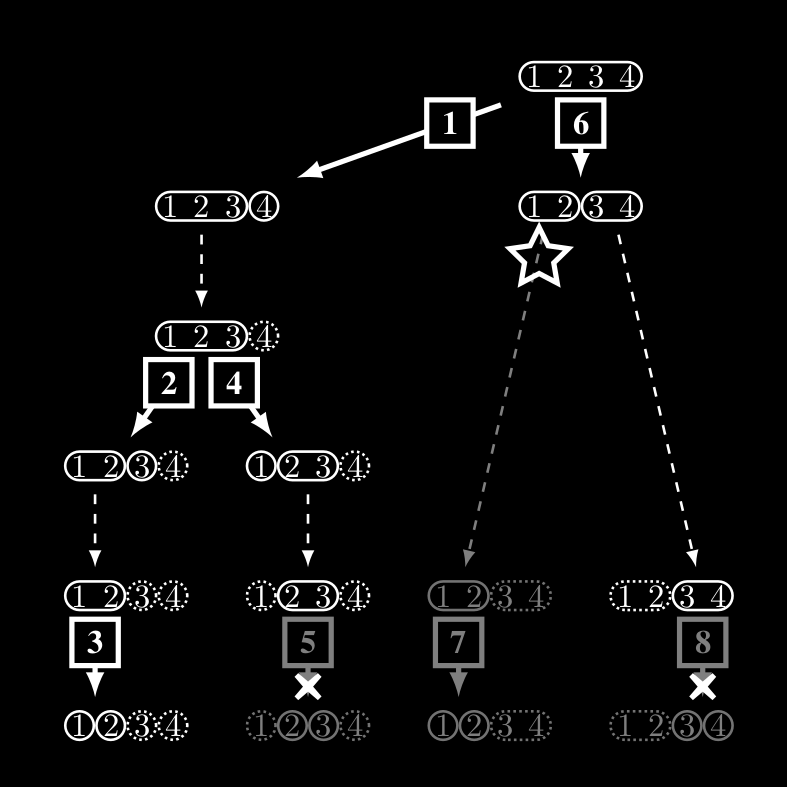
Because the dynamics of complex systems is the result of both decisive local events and reinforced global effects, the prediction of such systems could not do without a genuine multilevel approach. This paper proposes to found such an approach on information theory. Starting from a complete microscopic description of the system dynamics, we are looking for observables of the current state that allows to efficiently predict future observables.

Using the framework of the Information Bottleneck method, we relate optimality to two aspects: the complexity and the predictive capacity of the retained measurement. Then, with a focus on Agent-based Models, we analyse the solution space of the resulting optimisation problem in a generic fashion. We show that, when dealing with a class of feasible measurements that are consistent with the agent structure, this solution space has interesting algebraic properties that can be exploited to efficiently solve the problem. We then present results of this general framework for the Voter Model with several topologies and show that, especially when predicting the state of some sub-part of the system, multilevel measurements turn out to be the optimal predictors.

Télécharger l’article

Télécharger les diaposistives

Télécharger le poster

An Information-theoretic Framework for the Lossy Compression of Link Streams

Robin Lamarche-Perrin. Theoretical Computer Science, vol. 806, p. 90-115. Elsevier B.V., Amsterdam, 2018.

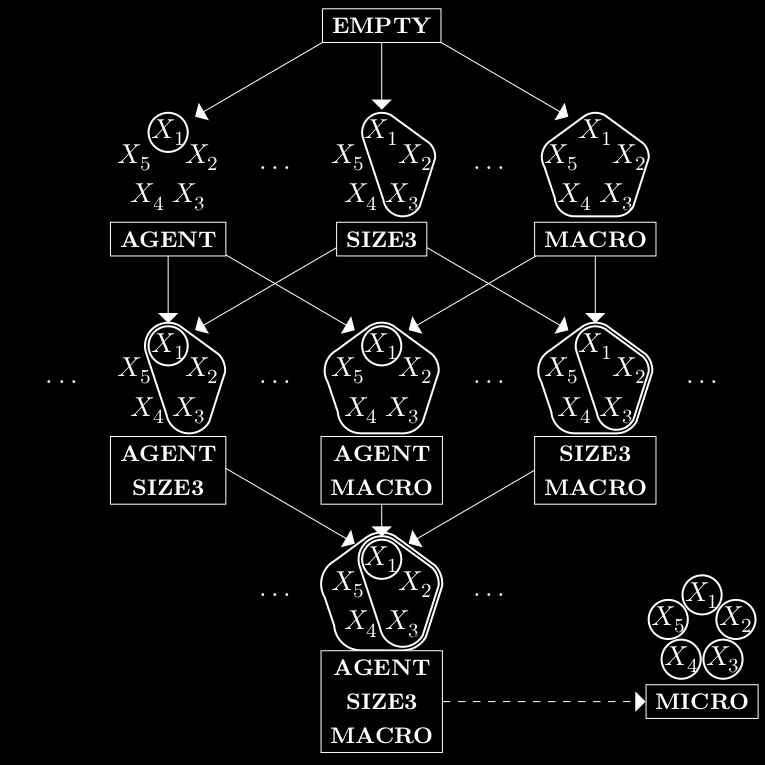
Graph compression is a data analysis technique that consists in the replacement of parts of a graph by more general structural patterns in order to reduce its description length. It notably provides interesting exploration tools for the study of real, large-scale, and complex graphs which cannot be grasped at first glance. This article proposes a framework for the compression of temporal graphs, that is for the compression of graphs that evolve with time.

This framework first builds on a simple and limited scheme, exploiting structural equivalence for the lossless compression of static graphs, then generalises it to the lossy compression of link streams, a recent formalism for the study of temporal graphs. Such generalisation relies on the natural extension of (bidimensional) relational data by the addition of a third temporal dimension. Moreover, we introduce an information-theoretic measure to quantify and to control the information that is lost during compression, as well as an algebraic characterisation of the space of possible compression patterns to enhance the expressiveness of the initial compression scheme. These contributions lead to the definition of a combinatorial optimisation problem, that is the Lossy Multistream Compression Problem, for which we provide an exact algorithm.

Télécharger l’article

Télécharger les diapositives

Télécharger le poster

Measuring Diversity in Heterogeneous Information Networks

Pedro Ramaciotti Morales, Robin Lamarche-Perrin, Raphaël Fournier-S’niehotta, Rémy Poulain, Lionel Tabourier, and Fabien Tarissan. ArXiv, 2020.

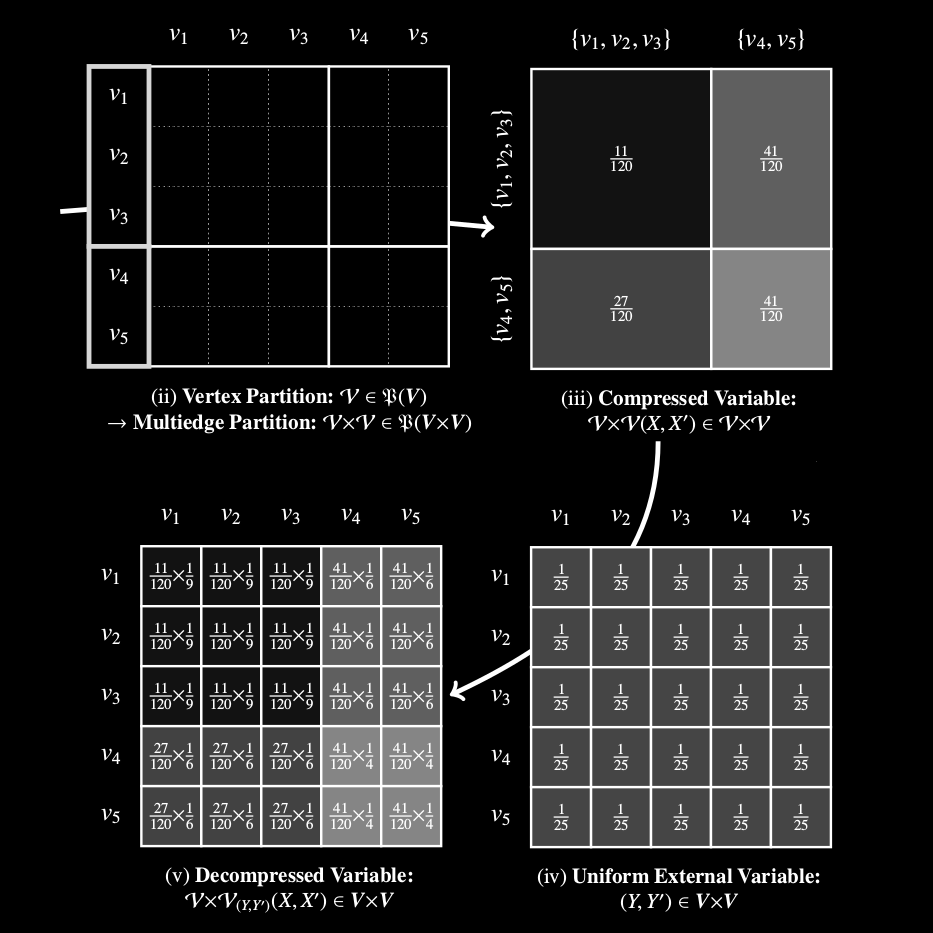
Diversity is a concept relevant to numerous domains of research varying from ecology, to information theory, and to economics, to cite a few. It is a notion that is steadily gaining attention in the information retrieval, network analysis, and artificial neural networks communities. While the use of diversity measures in network-structured data counts a growing number of applications, no clear and comprehensive description is available for the different ways in which diversities can be measured.

In this article, we develop a formal framework for the application of a large family of diversity measures to heterogeneous information networks (HINs), a flexible, widely-used network data formalism. This extends the application of diversity measures, from systems of classifications and apportionments, to more complex relations that can be better modeled by networks. In doing so, we not only provide an effective organization of multiple practices from different domains, but also unearth new observables in systems modeled by heterogeneous information networks. We illustrate the pertinence of our approach by developing different applications related to various domains concerned by both diversity and networks. In particular, we illustrate the usefulness of these new proposed observables in the domains of recommender systems and social media studies, among other fields.

Télécharger l’article

Télécharger les diapositives

Optimisation combinatoire

A Generic Algorithmic Framework to Solve Special Versions of the Set Partitioning Problem

Robin Lamarche-Perrin, Yves Demazeau and Jean-Marc Vincent. Research Report 105/2014, Max-Planck-Institute for Mathematics in the Sciences, Leipzig, Germany, 2014.

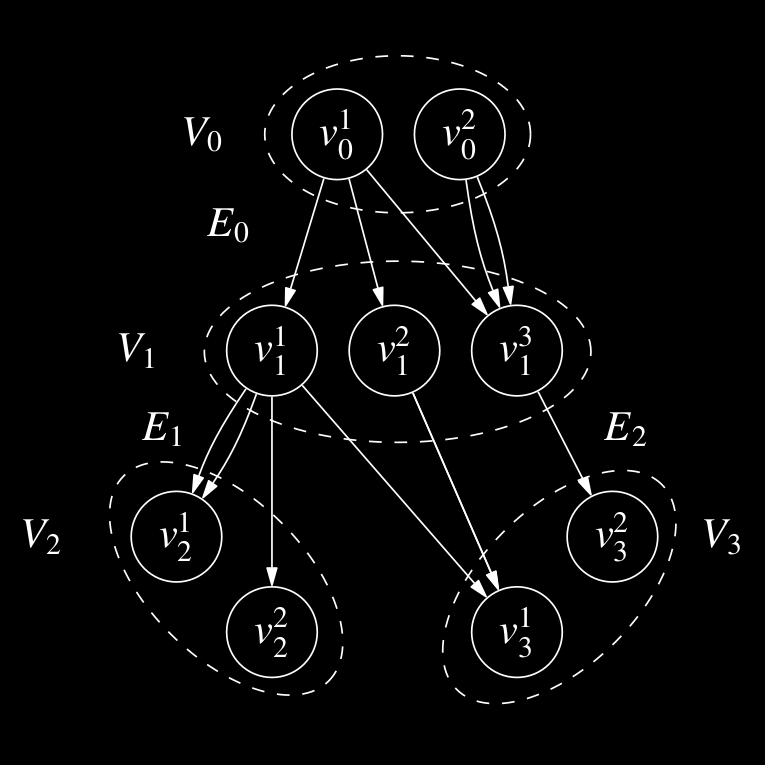
Given a set of individuals, a collection of admissible subsets, and a cost associated to each of these subsets, the Set Partitioning Problem (SPP) consists in selecting admissible subsets to build a partition of the individuals that minimizes the total cost. This combinatorial optimization problem has been used to model dozens of problems arising in specific domains of Artificial Intelligence and Operational Research, such as coalition structures generation, community detection, multilevel data analysis, workload balancing, image processing, and database optimization.

All these applications are actually interested in special versions of the SPP: the admissible subsets are assumed to satisfy global algebraic constraints derived from topological or semantic properties of the individuals. For example, admissible subsets might form a hierarchy when modeling nested structures, they might be intervals in the case of ordered individuals, or rectangular tiles in the case of bidimensional arrays. Such constraints structure the search space and – if strong enough – they allow to design tractable algorithms for the corresponding optimization problems. However, there is a major lack of unity regarding the identification, the formalization, and the resolution of these strongly-related combinatorial problems. To fill the gap, this article proposes a generic framework to design specialized dynamic-programming algorithms that fit with the algebraic structures of any special versions of the SPP. We show how to apply this framework to two well-known cases, namely the Hierarchical SPP and the Ordered SPP, thus opening a unified approach to solve versions that might arise in the future.

Télécharger l’article

Télécharger les diapositives