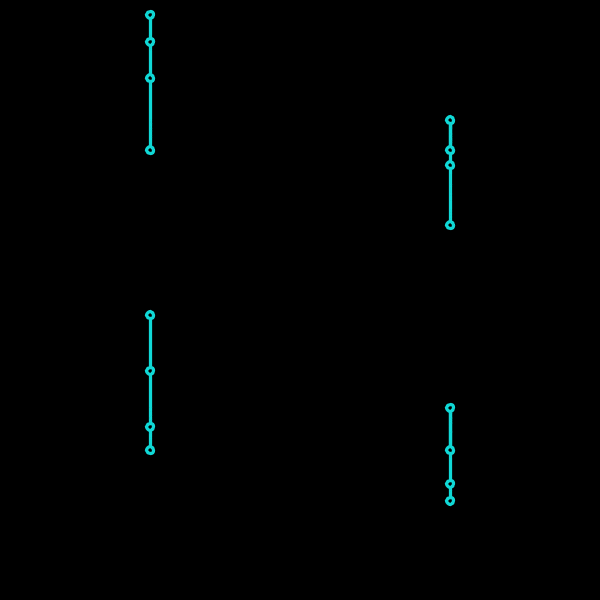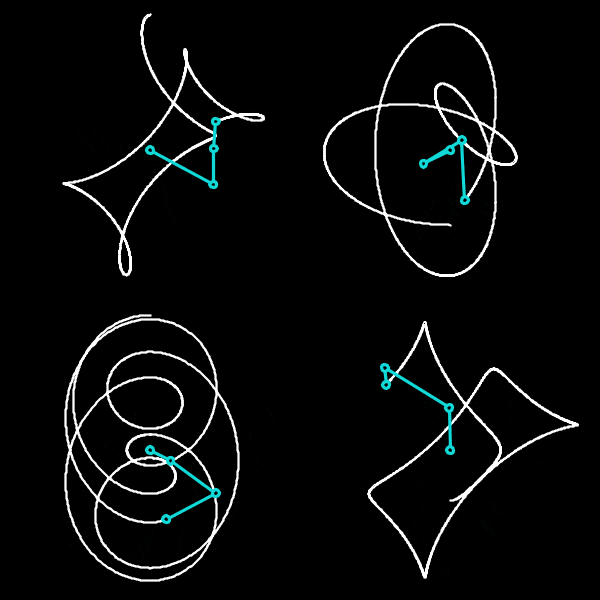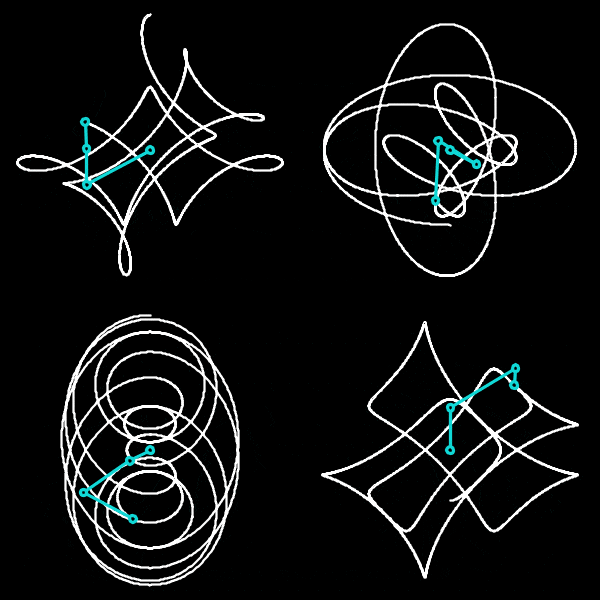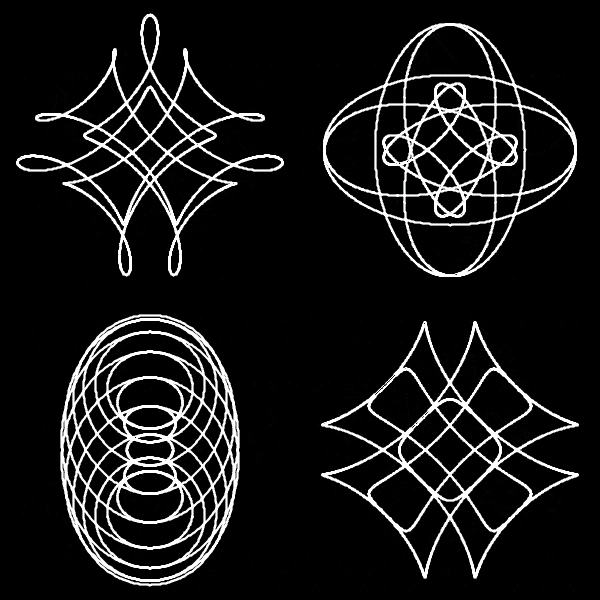
Les tritrochoïdes centrés constituent une famille de courbes fermées, engendrées par la rotation uniforme de trois axes mis bout à bout. La longueur de ces axes, ainsi que leur vitesse angulaire, offrent six paramètres simples desquels émergent une variété sans borne de figures géométriques singulières.
Espace des paramètres

Le cercle constitue évidemment le cas particulier le plus simple de cette famille géométrique. Les bitrochoïdes centrées, obtenus par le spirographe, résultent de la superposition de deux axes de rotation. Si le saut de complexité séparant le cercle du spirographe est déjà une surprise pour l’observateur, celui qui sépare le spirographe des tritrochoïdes centrés est plus difficile encore à appréhender.
Et pourtant, les six paramètres du système se résument à quatre paramètres indépendants (seul le rapport des longueurs et des vitesses angulaires compte). Quatre paramètres suffisent à décrire les membres d’une famille apparemment infinie.

Superposition
Le léger ajustement d’un paramètre induit une perturbation locale des courbes obtenues. La superposition d’une courbe et de son voisinage permet alors de déployer à l’image une petite portion de l’espace des paramètres, ajoutant à ces objets bidimensionnelles une nouvelle impression de volume ou de profondeur.